Practice Our Piecewise Functions Again
Introduction to Piecewise Functions
Piecewise functions (or piece-wise functions) are but what they are named: pieces of different functions (sub-functions) all on one graph. The easiest way to think of them is if you drew more than one function on a graph, and you just erased parts of the functions where they aren't supposed to be (along the \(ten\)'s). Thus, the \(y\)'due south are defined differently, depending on the intervals where the \(x\)'s are.
Notation that at that place is an example of a piecewise function'due south changed hither in the Inverses of Functions section.
Here's an example and graph:
| Piecewise Function | Graph |
| \(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+eight\,\,\,\,\,&\text{ if }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ if }ten>-2\stop{align} \correct.\) (There are other ways to display this, such equally using a "for" instead of an "if", and using commas or semi-colons instead of the "if".) Domain:\(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range:\(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) |  |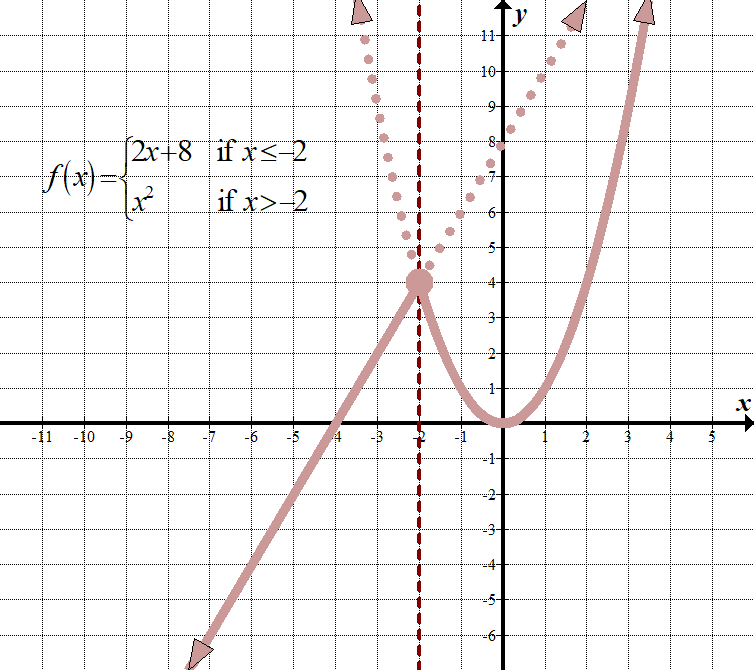
What this ways is for every \(x\) less than or equal to –two , we need to graph the line \(2x+viii\), as if it were the only role on the graph. For every \(10\) value greater than –2 , we need to graph \({{x}^{2}}\), as if it were the but function on the graph. Then we have to "go rid of" the parts that nosotros don't need.Call back that we however use the origin every bit the reference point for both graphs!
Encounter how the vertical line \(10=-2\) acts as a "purlieus" line betwixt the two graphs?
Note that the point \((–2,iv)\) has a airtight circle on it. Technically, it should only vest to the \(2x+8\) function, since that function has the less than or equal sign, but since the indicate is as well on the \({{x}^{ii}}\) graph, we tin can just utilize a airtight circumvolve every bit if it appears on both functions. See, non so bad, right?
Evaluating Piecewise Functions
Sometimes, you'll exist given piecewise functions and asked to evaluate them; in other words, detect the \(y\) values when you are given an \(ten\) value. Let's do this for \(ten=-6\) and \(x=four\)(without using the graph).Here is the function again:
\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ if }x\le -ii\\{{ten}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ if }x>-2\end{align} \correct.\)
We first desire to look at the conditions at the right get-go, to run into where our \(ten\)is. When \(x=-half dozen\), we know that it'due south less than –2 , and then we plug in our \(x\) to \(2x+eight\) only. \(f(ten)\) or \(y\) is \((2)(-half dozen)+eight=-four\). We don't even care nearly the \(\boldsymbol{{ten}^{2}}\)! It's that piece of cake. You tin can also see that nosotros did this correctly by using the graph above.
Now try \(x=4\). We await at the right first, and see that our \(ten\) is greater than –two , then we plug it in the \({{x}^{two}}\). (We can just ignore the \(2x+8\) this time.) \(f(x)\) or \(y\) is \({{4}^{2}}=16\).
Graphing Piecewise Functions
Yous'll probably be asked to graph piecewise functions. Sometimes the graphs volition contain functions that are non-continuous or discontinuous, significant that y'all take to pick upwardly your pencil in the middle of the graph when you are cartoon information technology (like a jump!).Continuous functions means that you never have to pick up your pencil if yous were to draw them from left to right.
And recollect that the graphs are true functions only if they pass the Vertical Line Test.
Allow'due south draw these piecewise functions and decide if they are continuous or non-continuous. Notation how we describe each office as if it were the only i, and then "erase" the parts that aren't needed. We'll as well get the Domain and Range like we did hither in the Algebraic Functions department.
| Piecewise Part | Graph |
| \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\text{if }x\le iv\\\frac{1}{2}ten-two\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range:\(\left( {0,\infty } \correct)\) |  |
| \(\displaystyle f\left( 10 \right)=\left\{ \begin{assortment}{l}x+4\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if one}\le 10<4\\ten-5\,\,\,\,\,\,\,\,\,\text{if }ten\ge 4\terminate{array} \right.\) Non-Continuous Domain:\(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) |  |
We can actually put piecewise functions in the graphing calculator:
| Piecewise Function Screens | Steps and Notes |
| Enter the piecewise office on 3 lines: Hither's the graph: | To put the piecewise part\(\displaystyle f\left( 10 \right)=\left\{ \begin{array}{l}ten+4\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le x<4\\-5+x\,\,\,\,\,\text{if }x\ge 4\cease{array} \right.\) in the figurer, you tin can enter the function on iii lines by dividing the function in each interval by a "exam inequality" of that interval (and sentinel parentheses!). The reason we split by the intervals or inequalities is because the calculator will return a 1 if the inequality (such equally \(x<1\)) is true; for example, \((10+4)\) volition just end up \((x+4)/(one)\) when \(ten<1\). When \(x\ge 1\), nosotros are dividing by 0 , so nothing volition be drawn. Hither is what we can put in the calculator: \(\displaystyle \begin{assortment}{l}{{Y}_{1}}=\left( {x+four} \right)/\left( {x<one} \right)\\{{Y}_{ii}}=\left( two \right)/\left( {x\ge 1\text{ and }x<4} \right)\\{{Y}_{3}}=\left( {-5+x} \correct)/\left( {ten\ge iv} \right)\end{array}\) Note that yous can also enter this on one line by multiplying the weather instead of dividing, and using plus signs between each of the three functions/intervals: \(\displaystyle {{Y}_{1}}=\left( {x+4} \right)\left( {x<1} \right)+\left( ii \correct)\left( {x\ge i\text{ and }x<iv} \correct)+\left( {-5+x} \right)\left( {x\ge four} \right)\). Here are the keystrokes for using iii lines. Notation that y'all use twond MATH (Test) to get to the screen that has the \(\le \), \(\ge \), so on. For example, 2nd MATH 6 gets you \(\le \). Use 2nd MATH (TEST), right to LOGIC, then 1, for the "and" in \({{Y}_{2}}\). |
How to Tell if Piecewise Part is Continuous or Non-Continuous
To tell if a piecewise graph is continuous or non-continuous, you can look at the purlieus points and see if the \(y\) betoken is the same at each of them. (If the \(y\)'s were different, there'd be a "jump" in the graph!)
Endeavour this for the functions we used higher up:
| Piecewise Role | Check Boundary Points |
| \(\displaystyle f\left( x \correct)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\,\text{if }10\le 4\\\frac{1}{2}x-ii\,\,\,\,\,\,\,\,\,\,\text{if }x>iv\end{array} \right.\) | Check \(10=4\) in both parts of the function, since four is the "boundary point": \(\begin{array}{l}-two(four)+8=0\\\,\,\,\frac{one}{2}(4)-ii=0\end{array}\) Since \(0=0\), this piecewise office is continuous. |
| \(\displaystyle f\left( x \correct)=\left\{ \begin{assortment}{50}ten+4\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le 10<iv\\-v+x\,\,\,\,\,\,\,\,\,\text{if }x\ge 4\terminate{assortment} \right.\) | Bank check \(ten=1\) in the commencement two parts of the function. Note in the second part, \(y\) is always 2 : \(\begin{array}{l}1+4=5\\\,\,\,\,\,\,\,\,\,two=ii\end{assortment}\) Since \(5\ne 2\), we can end here, and notation that this piecewise function is non-continuous. If the \(y\)'s were equal, nosotros'd have to go ane to bank check the next boundary betoken at \(x=4\). |
Obtaining Equations from Piecewise Role Graphs
You may be asked to write a piecewise role, given a graph. Now that we know what piecewise functions are all about, it'southward non that bad! To review how to obtain equations from linear graphs, see Obtaining the Equations of a Line, and from quadratics, see Finding a Quadratic Equation from Points or a Graph.
Here are the graphs, with explanations on how to derive their piecewise equations:
| Piecewise Function Graph | Process to get Function |
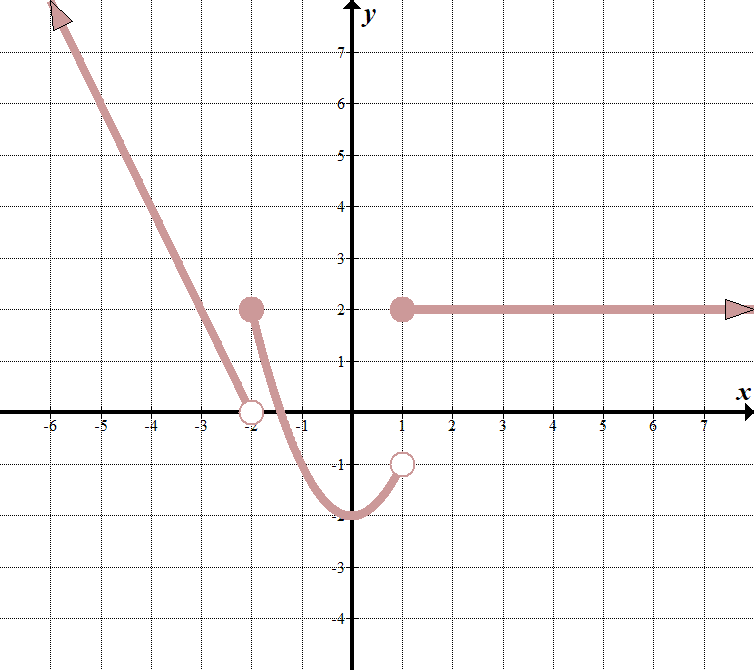 | Nosotros see that our "boundary lines" are at \(x=-two\) and \(x=1\). We know that our office volition expect something like this (notice open and closed endpoints): \(\displaystyle f\left( x \right)=\left\{ \begin{assortment}{fifty}\text{ }……\,\,\,\,\,\,\,\,\text{if }x<-2\\\text{ }……\,\,\,\,\,\,\,\,\text{if }-\text{2 }\le x<1\\\text{ }……\,\,\,\,\,\,\,\,\text{if }x\ge ane\end{array} \right.\) Pick two points \((–2,0)\) and \((–3,two)\) on the leftmost line to get the equation \(y=-2x-4\). The middle function is \(y={{ten}^{ii}}-ii\), and the rightmost role is just the horizontal line \(y=2\). Thus, the piecewise function is: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x-four\,\,\,\,\,\,\,\text{if }ten<-2\\\text{ }{{ten}^{two}}-2\,\,\,\,\,\,\,\,\,\,\text{if }-\text{2}\le 10<1\\\text{ 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }ten\ge ane\end{array} \right.\) |
 | Nosotros see that our "boundary line" is at \(x=v\). Since the lines see at \((five,4)\), it doesn't matter where we put the \(\le \) or \(\ge \) sign; we but tin't put it both places, or it wouldn't exist a office. Nosotros have and then far: \(\displaystyle f\left( x \correct)=\left\{ \begin{assortment}{l}\text{ }……\,\,\,\,\,\,\,\,\,\text{if }x<5\\\text{ }……\,\,\,\,\,\,\,\,\,\text{if }x\ge v\end{array} \right.\) Again, we accept to look at each line separately to determine their equations. Either have 2 points from each line to get these, or derive from slopes and \(y\) – intercepts; the piecewise part is: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{fifty}\frac{vi}{5}x-2\,\,\,\,\,\,\,\text{if }x<5\\\frac{2}{5}10+two\,\,\,\,\,\,\,\text{if }10\ge 5\end{assortment} \correct.\) |
Absolute Value as a Piecewise Function
You may be asked to write an absolute value function as a piecewise office. You lot might want to review Solving Absolute Value Equations and Inequalities before continuing on to this topic.
Let'south say we take the function\(f\left( 10 \correct)=\left| 10 \right|\). From what we learned earlier, we know that when \(ten\) is positive, since we're taking the absolute value, it will still only exist \(ten\). But when \(x\) is negative, when nosotros take the absolute value, we accept to take the reverse (negate information technology), since the accented value has to exist positive. Make sense? So, for example, if we had \(|5|\), we merely take what'due south inside the accented sign, since it'due south positive. Just for \(|–5|\), nosotros have to take the opposite (negative) of what'southward inside the absolute value to make it \(\displaystyle five\,\,(–five=5)\).
This ways we can write this absolute value office as a piecewise function. Notice that we can get the "turning bespeak" or "boundary point" by setting whatever is inside the absolute value to 0. Then we'll either use the original function, or negate the part, depending on the sign of the function (without the absolute value) in that interval.
For example, we can write \(\displaystyle \left| ten \right|=\left\{ \begin{array}{l}ten\,\,\,\,\,\,\,\,\,\text{if }x\ge 0\\-x\,\,\,\,\,\text{if }10<0\end{array} \right.\). Likewise annotation that, if the part is continuous (in that location is no "jump") at the boundary point, it doesn't matter where we put the "less than or equal to" (or "greater than or equal to") signs, as long as nosotros don't repeat them! We can't echo them because, theoretically, we can't have two values of \(y\) for the same \(x\), or we wouldn't have a function.
Here are more than examples, with explanations. You can also check these in the graphing computer using \({{Y}_{1}}=\) and MATH NUM ane (abs). (Yous might want to review Quadratic Inequalities for the second example below):
| Absolute Value Function | Method to get Piecewise Function |
| \(g\left( x \right)=\left| {2x+iii} \right|\) | First notice the "boundary line". We exercise this by setting what'south inside the absolute value to 0, and then solving for \(\boldsymbol{10}\). When \(2x+three\ge 0\), nosotros go \(\displaystyle x\ge -\frac{3}{2}\) (actually, nosotros can keep the \(\ge \) when we solve). When \(2x+iii\) is positive (not-negative, really), we only take information technology "equally is", but if it'southward negative, we have to negate the whole affair. Therefore, the piecewise role is: \(\displaystyle \left| {2x+three} \right|=\left\{ \begin{array}{l}2x+iii\,\,\,\,\,\,\,\,\,\text{if }x\ge -\frac{three}{2}\text{ }\\-2x-3\,\,\,\,\,\text{if }x<-\frac{3}{2}\end{assortment} \right.\) Try it – information technology works! |
| \(f\left( x \right)=\left| {{{x}^{2}}-4} \right|\) | First find the "boundary line(s)"; nosotros set what'south within the absolute value to 0 . When \({{x}^{ii}}-four\ge 0\), we get \(ten\le -two\) or \(x\ge 2\) (attempt some numbers!). When \({{x}^{ii}}-four\) is positive (non-negative, really), we just take it "every bit is", but if it'south negative, we have to negate it. The piecewise function is: \(\displaystyle \left| {{{x}^{ii}}-four} \correct|=\left\{ \begin{array}{l}{{x}^{2}}-iv\,\,\,\,\,\text{if }x\le -2\\4-{{x}^{2}}\,\,\,\,\,\text{if }-two<x<2\\{{x}^{2}}-4\,\,\,\,\,\text{if }10\ge 2\text{ }\end{array} \correct.\) or \(\displaystyle \left| {{{x}^{2}}-4} \correct|=\left\{ \brainstorm{array}{l}{{ten}^{ii}}-4\,\,\,\,\,\,\text{if }ten\le -2\text{ }\,\,\text{or}\,\,\text{ }x\ge 2\\4-{{x}^{ii}}\,\,\,\,\,\,\,\text{if }-ii<10<2\cease{assortment} \right.\) Again (since the function is continuous), it really doesn't matter where we accept the \(\le \) and \(\ge \) (as opposed to \(<\) and \(>\)), every bit long every bit nosotros don't repeat them. |
| \(f\left( x \right)=2x+\left| {x+two} \right|\) | This one's a trivial trickier, since nosotros accept an \(ten\) inside and outside the absolute value. For the "purlieus line", we only use what is inside the absolute value. When \(x+2\ge 0\), we get \(10\ge -2\). When \(10+2\) is positive (non-negative, actually) (\(ten\ge -ii\)), nosotros only accept it "as is", but if it's negative, we take to negate it to arrive \(-x-two\). For the piecewise office, we have to utilize the whole part, including the part that's outside the absolute value. And then, the piecewise function is: \(\displaystyle 2x+\left| {ten+two} \right|=\left\{ \brainstorm{array}{l}2x+x+2\,\,\,\,\,\text{if }x\ge -2\\2x-x-2\,\,\,\,\,\text{if }x<-ii\end{array} \right.\) Simplify: \(\displaystyle 2x+\left| {x+2} \right|=\left\{ \brainstorm{array}{fifty}3x+2\,\,\,\,\,\,\,\text{if }x\ge -2\\x-ii\,\,\,\,\,\,\,\,\,\,\text{if }x<-2\end{array} \right.\) Endeavour some values less than and great then –2 ; they should work! |
| \(thousand\left( 10 \right)=\left| {{{ten}^{two}}-4x-5} \correct|\) | This one is all-time solved with a sign nautical chart since we have a quadratic and nosotros demand to know where the office is positive and negative. Get-go, factor the quadratic inside the absolute value part to \(\left( {10-five} \right)\left( {x+1} \right)\). Then use a sign chart to meet where the factors are positive and negative, and retrieve that where the factors are positive (non-negative, actually), we use the role "as is", and where the factors are negative, nosotros negate the part: \(\displaystyle \left| {{{x}^{ii}}-4x-5} \right|=\left\{ \begin{array}{l}{{x}^{2}}-4x-five\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }x\le -ane\,\,\,\,\text{or}\,\,\,\,x\ge 5\\-{{x}^{2}}+4x+five\,\,\,\,\,\,\,\,\,\text{if }-one<x<5\text{ }\end{array} \right.\) |
| \(\displaystyle thousand\left( x \right)=\frac{{\left| {ten+2} \right|}}{{x+2}}\) | This is a rational function, since there's a variable in the denominator. When \(x+2\ge 0\), nosotros get \(\displaystyle x\ge -two\). When \(x+2\) is positive (non-negative, actually), we but have it "as is", but if it'southward negative, we accept to negate what's in the absolute value: \(\displaystyle \frac{{\left| {x+two} \correct|}}{{x+2}}=\left\{ \begin{array}{50}\frac{{x+2}}{{x+2}}\,\,(=1)\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }x\ge -2\\\frac{{-x-2}}{{x+ii}}\,\,(=-1)\,\,\,\,\,\,\text{if }x<-2\terminate{array} \right.\). But nosotros accept to be careful, since \(x\ne 2\) (domain restriction: the denominator would be 0 ). Therefore, the piecewise function is: \(\displaystyle \frac{{\left| {x+2} \right|}}{{x+ii}}=\left\{ \begin{array}{fifty}i\,\,\,\,\,\,\,\,\,\,\text{if }x>-two\\-one\,\,\,\,\,\,\text{if }x<-2\end{assortment} \right.\). |
You may too be asked to take an absolute value graph and write it every bit a piecewise function:
| Absolute Value Graph | Method to get Piecewise Function |
 | We see that our "boundary line" is at \(x=0\), so what'southward inside the absolute value sign must be \(10\) or a factor of \(ten\). (This is because to get the purlieus line with an absolute value function, we prepare what's inside the accented value to 0 , and solve for \(x\)). When \(ten>0\), nosotros can run into that the equation of the line is \(y=2x-2\). When \(10<0\), the equation is \(y=-2x-two\). We tin can write this as a piecewise function: \(\displaystyle f\left( x \right)=\left\{ \brainstorm{assortment}{l}2x-2\,\,\,\,\,\,\,\text{if }x>0\\-2x-ii\,\,\,\text{if }x\le 0\end{assortment} \right.\) We can also write this equally a transformed absolute value function: \(y=2\left| x \correct|-ii\) or \(y=\left| {2x} \right|-2\) (since 2 is positive, information technology tin can be inside or outside the \(\left| {\,\,} \right|\)). (This makes sense since when what'south within the \(\left| {\,\,} \right|\) is \(> 0\), we utilize the regular function \(y=2x-two\), and when what'southward inside the is \(< 0\), we negate the accented value part to make it \(y=-\left( {2x} \right)-2\)). |
 | We meet that our "purlieus lines" are at \(x=2\) and \(10=-2\), so what's inside the accented value sign must have factors of \(x-2\) and \(10+two\). When \(x<-2\) or \(x>ii\), we can meet that the graph looks like the normal function of the graph \(y={{x}^{two}}-4\). (I figured this out by knowing the factors, and taking a expert guess!) When \(-2<x<2\), the equation \(y={{x}^{2}}-4\) is flipped, or negated (flipped over the \(x\)-axis). Nosotros tin can write this as a piecewise function: \(\displaystyle f\left( x \right)=\left\{ \brainstorm{assortment}{l}{{10}^{ii}}-four\,\,\,\,\,\,\,\,\,\text{if }x<-two\text{ or }x>2\\-{{x}^{2}}\text{+ 4}\,\,\,\,\,\,\text{if }-2\le ten\le ii\finish{assortment} \right.\) We tin can see that this started out a transformed quadratic part \(y={{x}^{2}}-four\) with an absolute value around information technology, since all \(y\) values are positive: \(y=\left| {{{x}^{2}}-4} \right|\). |
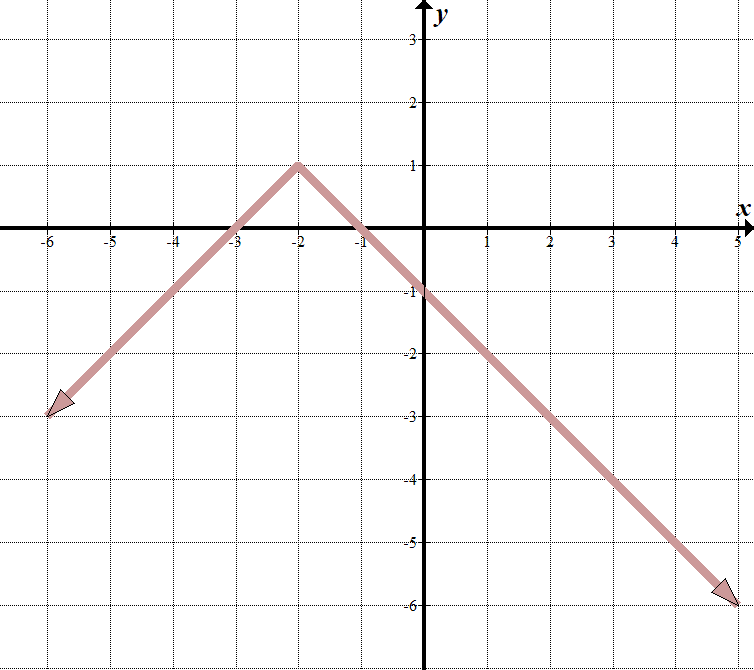 | We see that our "boundary line" is at \(ten=-two\), then what's inside the absolute value sign must exist \(x+2\). When \(10>-ii\), we can see that the equation of the line is \(y=-ten-i\). When \(10<-2\), the line is \(y=10+3\). Nosotros can write this as a piecewise function: \(\displaystyle f\left( 10 \correct)=\left\{ \brainstorm{array}{l}-x-one\,\,\,\,\,\,\text{if }ten>-2\\x+3\,\,\,\,\,\,\,\,\,\,\text{if }10\le -2\end{array} \right.\) It'southward probably easier to write this every bit a transformed absolute value function. Nosotros can see that the parent accented value function is flipped vertically, move to the left 2 , and upwards one . Our absolute value equation is \(y=-\left| {x+2} \right|\,\,+\,\,1\). This is the same equally the piecewise office above. Try it – it works! |
Transformations of Piecewise Functions
Let's exercise a transformation of a piecewise function. We learned how about Parent Functions and their Transformations hither in the Parent Graphs and Transformations department. You'll probably want to read this section first, before trying a piecewise transformation. Let's transform the post-obit piecewise function flipped around the \(x\)-centrality, vertically stretched by a factor of 2 units, 1 unit to the correct, and 3 units up.
So, let's describe \(-2f\left( x-1 \right)+3\), where:
\(\displaystyle f\left( 10 \right)=\left\{ \brainstorm{align}x+4\,\,\,\,\,\,\,\,&\text{ if }ten<1\\2\,\,\,\,\,\,\,\,&\text{ if 1 }\le x<4\\x-v\,\,\,\,\,\,\,\,&\text{ if }x\ge 4\cease{align} \right.\)
Make sure to use the "boundary" points when nosotros fill in the t-chart for the transformation. Retrieve that the transformations inside the parentheses are washed to the \(10\) (doing the opposite math), and outside are done to the \(y\). To come upward with a t-chart, as shown in the table below, we can employ key points, including 2 points on each of the "purlieus lines".
Note that because this transformation is complicated, we tin come up with a new piecewise function by transforming the iii "pieces" and as well transforming the "\(x\)"s where the boundary points are (adding 1 , or going to the correct 1 ), since we do the opposite math for the "\(x\)"south. To get the new functions in each interval, we can just substitute "\(x-ane\)" for "\(x\)" in the original equation, multiply by –2 , and so add 3 . For instance, for the first part of the piecewise function, \(\displaystyle -2f\left( {x-1} \right)+iii=-2\left[ {\left( {x-ane} \right)+4} \right]+3=-2\left( {x+three} \right)+3=-2x-3\). Then we have:
\(\displaystyle -2f\left( {x-1} \correct)+3=\left\{ \begin{array}{l}-two\left( {\left( {ten-ane} \right)+four} \right)+iii=-2x-3,\,\,\,\,\text{ }\,\,\text{ if }x-one<i\,\,\,\,\left( {x<2} \correct)\\-2\left( 2 \right)+3=-1,\,\,\,\,\text{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{ if }\,\text{ 2 }\le x<five\\-2\left( {\left( {x-1} \correct)-five} \correct)+iii=-2x+15,\,\,\,\,\,\,\text{ if }x\ge v\terminate{assortment} \right.\)
Hither are the "before" and "later on" graphs, including the t-nautical chart:
| Piecewise Parent Part | T-chart | Transformation of Function | ||||||||||||||||||||||||||||||||||||||||
| \(\displaystyle f\left( x \correct)=\left\{ \begin{array}{l}ten+4\,\,\,\,\,\,\,\,\text{if }10<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le 10<4\\x-v\,\,\,\,\,\,\,\,\text{if }ten\ge 4\end{array} \right.\) |
| \(\displaystyle -2f\left( {10-i} \right)+iii=\left\{ \begin{assortment}{l}-2x-3\,\,\,\,\,\,\,\,\,\text{if }x<2\\-ane\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 2}\le x<v\\-2x+15\,\,\,\,\,\,\text{if }x\ge 5\end{array} \right.\) | ||||||||||||||||||||||||||||||||||||||||
Piecewise Function Discussion Problems
Trouble:
Your favorite domestic dog groomer charges according to your domestic dog's weight. If your domestic dog is xv pounds and under, the groomer charges $35 . If your domestic dog is between 15 and 40 pounds, she charges $40 . If your canis familiaris is over 40 pounds, she charges $40 , plus an additional $2 for each pound.
(a) Write a piecewise function that describes what your dog groomer charges. (b) Graph the function. (c) What would the groomer charge if your canis familiaris weighs threescore pounds?
Solution:
(a) We meet that the "boundary points" are 15 and twoscore , since these are the weights where prices alter. Since nosotros have two boundary points, we'll have three equations in our piecewise function. Nosotros have to start at 0 , since dogs have to counterbalance over 0 pounds:
\(\displaystyle f\left( x \right)=\left\{ \begin{assortment}{50}\text{ }……\,\,\,\,\,\,\,\,\,\text{if }0<x\le 15\\\text{ }……\,\,\,\,\,\,\,\,\,\text{if }15<x\le xl\\\text{ }……\,\,\,\,\,\,\,\,\,\text{if }ten>twoscore\end{array} \right.\)
We are looking for the "answers" (how much the grooming costs) to the "questions" (how much the domestic dog weighs) for the iii ranges of prices. The first two are just flat fees ( $35 and $40 , respectively). The final equation is a picayune trickier; the groomer charges $forty plus $2 for each pound over twoscore . Permit's try existent numbers: if your dog weighs threescore pounds, she will charge $40 plus $2 times \(xx\,\,(60–twoscore)\). We'll plough this into an equation: \(40+2(x–40)\), which simplifies to \(2x–xl\) (see how two is the gradient?).
The whole piecewise function is:
\(\displaystyle f\left( ten \right)=\left\{ \begin{assortment}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }0<x\le 15\\\text{ }xl\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }xv<x\le 40\\\text{ }forty+2\left( {x-40} \right)\,\,\,\,\,\,\text{if }ten>forty\end{array} \right.\) or \(\displaystyle f\left( x \correct)=\left\{ \brainstorm{array}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }0<10\le 15\\\text{ }forty\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }xv<x\le forty\\\text{ }2x-40\,\,\,\,\,\,\,\text{if }x>40\stop{assortment} \right.\)
(b) Permit's graph: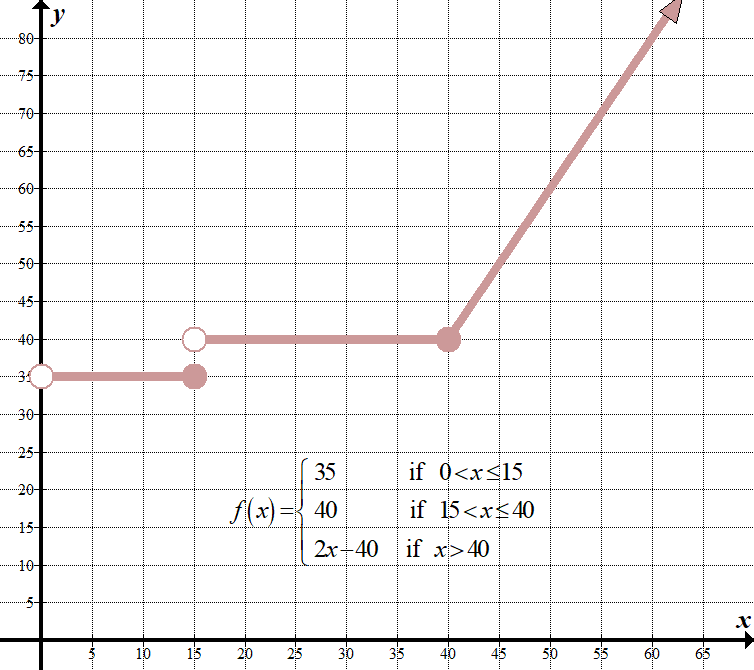
Note that this piecewise equation is non-continuous. Also notation a reasonable domain for this problem might be \(\left( {0,200} \right]\) (given dogs don't counterbalance over 200 pounds!) and a reasonable range might be \(\left[ {35} \right]\cup \left[ {40,360} \right]\).
(c) If your dog weighs 60 pounds, we can either employ the graph, or the part to see that you would have to pay $eighty .
Problem:
You plan to sell t-shirts as a fundraiser. The wholesale t-shirt company charges you $10 a shirt for the first 75 shirts. After the first 75 shirts you purchase up to 150 shirts, the visitor volition lower its price to $vii.fifty per shirt. After you purchase 150 shirts, the price will decrease to $5 per shirt. Write a function that models this state of affairs.
Solution:
We see that the "boundary points" are 75 and 150 , since these are the number of t-shirts bought where prices change. Since we have two boundary points, we'll take three equations in our piecewise function. We'll commencement with \(x\ge i\), since, we assume at least one shirt is bought. Note in this problem, the number of t-shirts bought (\(x\)), or the domain, must be a integer, simply this restriction shouldn't bear upon the outcome of the problem.
\(\displaystyle f\left( x \right)=\left\{ \begin{assortment}{fifty}\text{ }……\text{ if }1\le x\le 75\\\text{ }……\text{ if }75<ten\le 150\\\text{ }……\text{ if }x>150\end{array} \right.\)
Nosotros are looking for the "answers" (total cost of t-shirts) to the "questions" (how many are bought) for the three ranges of prices.
For upwardly to and including 75 shirts, the price is $10 , so the total price would \(10x\). For more 75 shirts only up to 100 shirts, the price is $7.50 , but the beginning 75 t-shirts will nonetheless cost $10 per shirt. The 2nd function includes the $750 spent on the first 75 shirts ( 75 times $10 ), and also includes $vii.50 times the number of shirts over 75 , which would be \((x-75)\). For example, if you bought 80 shirts, yous'd have to spend \(\$10\times 75=\$750\), plus \(\$seven.50\times 5\,\) (eighty – 75) for the shirts later on the 75th shirt.
Similarly, for over 150 shirts, we would withal pay the $10 price up through 75 shirts, the $7.50 cost for 76 to 150 shirts ( 75 more than shirts), and then $five per shirt for the number of shirts bought over 150 . We'll pay \(10(75)+7.50(75)+5(x-150)\) for \(x\) shirts. Put in numbers and try it!
The whole piecewise function is:
\(\displaystyle f\left( x \right)=\left\{ \brainstorm{assortment}{l}\text{ }10x\text{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }1\le 10\le 75\\\text{ 10}\left( {75} \right)+vii.v\left( {x-75} \correct)\text{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{ if 7}v<x\le 150\\\text{ 10}\left( {75} \right)+seven.five\left( {75} \right)+5\left( {10-150} \right)\text{ }\,\text{if }x>150\end{array} \correct.\) or \(\displaystyle f\left( x \right)=\left\{ \begin{array}{50}\text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }1\le 10\le 75\\\text{ }vii.5x\text{ }+\text{ }187.5\,\,\,\,\,\text{if 7}5<x\le 150\\\text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\,\text{if }ten>150\end{assortment} \right.\)
Trouble:
A bus service costs $fifty for the kickoff 400 miles, and each boosted 300 miles (or a fraction thereof) adds $10 to the fare. Use a piecewise part to represent the bus fare in terms of the distance in miles.
Solution:
This is actually a tricky problem, merely allow's get-go retrieve offset nigh the "boundary point", which is 400 . Information technology'due south pretty straightforward when the ride is less than 400 miles; the cost is $50 .
For greater than 400 miles, we have to subtract out the showtime 400 miles (merely recall to include the first $l ), divide the number of miles left past 300 miles (and round upwardly, if at that place'due south a partial amount), and multiply that by $10 .
The tricky part is when nosotros "circular up" for a portion of the side by side 300 miles. We can use a "ceiling" role (designated by \(\left\lceil {} \right\rceil \)); this office gives the to the lowest degree integer that is greater than or equal to its input; for example, the ceiling of both iii.5 and 4 is four .
Thus, this is what we have:
\(\displaystyle f\left( x \right)=\left\{ \begin{assortment}{l}\text{ }50\text{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }0\le x\le 400\\\text{ }fifty+\left( {10\times \left\lceil {\frac{{x-400}}{{300}}} \correct\rceil } \right)\text{ }\,\,\,\,\,\text{ if }x>400\end{assortment} \correct.\)
Permit'southward attempt it! If we accept a 1500 -mile ride, the price would be \(\displaystyle 50+\left( {x\times \left\lceil {\frac{{1500-400}}{{300}}} \correct\rceil } \correct)\text{ }=50+\left( {10\times 4} \correct)=\$90\).
Problem:
What value of \(\boldsymbol{a}\) would make this piecewise function continuous?
\(\displaystyle f\left( x \right)=\left\{ \brainstorm{array}{50}3{{x}^{2}}+4\,\,\,\,\,\text{ if }x<-2\\5x+\boldsymbol{a}\,\,\,\,\,\,\,\,\text{if }x\ge -two\end{array} \right.\)
Solution:
For the piecewise part to be continuous, at the boundary point (where the function changes), the two \(y\) values must be the same. Nosotros can plug in –2 for \(ten\) in both of the functions and make sure the \(y\)'s are the aforementioned
\(\brainstorm{marshal}3{{x}^{2}}+4&=5x+a\\3{{\left( {-2} \correct)}^{two}}+4&=5\left( {-two} \correct)+a\\12+4&=-10+a\\a&=26\end{align}\)
If \(a=26\), the piecewise function is continuous!
Learn these rules, and practice, practice, do!
More than Practice: Employ the Mathway widget below to attempt write a Piecewise Function. Click on Submit (the blue pointer to the right of the problem) and click on Write the Absolute Value as Piecewiseto see the answer.
Y'all can too blazon in your own problem, or click on the three dots in the upper correct hand corner and click on "Examples" to drill down past topic.
If you lot click on Tap to view steps, or Click Hither, you can register at Mathway for a free trial, and then upgrade to a paid subscription at whatsoever time (to become any type of math problem solved!).
On to Matrices and Solving Systems with Matrices – yous are ready!
Source: https://mathhints.com/piecewise-functions/
0 Response to "Practice Our Piecewise Functions Again"
ارسال یک نظر